Estimation of Coupling Constant, $J(z)$

The magnetisation vs temperature scans can be used to estimate the strength of the exchange coupling between the iron layers when they are antiferromagnetically coupled. Figure 7.7 shows an exploded view of an Fe/Ce/Fe section of a multilayer in an applied field.

Figure 7.7: Exploded view of a Ce/Fe multilayer showing the antiferromagnetic coupling between the iron layers.

Figure 7.8: Variation of antiferromagnetic coupling constant, $J(z)$, with cerium layer thickness, $z$. The dashed line, representing a theoretical picture of oscillatory coupling, is added to guide the eye.

In this system there is an energy, $W_{AFM}$, associated with the antiferromagnetic exchange coupling and an energy, $W_{H}$, from the applied field, $H$. These are related to the magnetisation of the iron layers by the following

$$W_{AFM} = -2J(z)\boldsymbol{M}_{1}\centerdot\boldsymbol{M}_{2}$$

$$W_{H} = -\boldsymbol{M}_{1}\centerdot\boldsymbol{H} - \boldsymbol{M}_{2}\centerdot\boldsymbol{H}$$

$$W = W_{AFM} + W_{H}$$ (7.1)

where $M_{1}$ and $M_{2}$ are the respective magnetisations of the two layers. In our systems we take the layer magnetisations to be equal, hence $M_{1} = M_{2} = M$. We can find the minimum in energy with respect to the angle $\phi$ between the applied field and the magnetisation, where $\nicefrac{\partial W}{\partial\phi}=0$. This yields the result

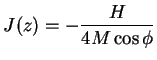$$J(z) = -\frac{H}{4M\cos\phi}$$ (7.2)

When the system is at $T_{N}$ the spins will be fully aligned with the applied field and $\phi=0$, hence

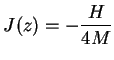$$J(z) = -\frac{H}{4M}$$ (7.3)

The magnetisation, $M$, can be read from the magnetisation vs temperature scans at the $T_{N}$ of each sample. As $J(z)$ is a function of the distance, $z$, between the two iron layers we would expect the values obtained to vary with the cerium layer thickness. This is likely to be an oscillatory dependence on separation distance between the magnetic layers similar to the RKKY interaction between magnetic atoms that has been observed in many transition metal systems[41]. The calculated $J(z)$ values are plotted in Figure 7.8.

The plot does show a variation with $z$ although with so few points the actual dependence upon $z$ cannot be calculated. The scans for the 40/20 sample appear to show either weak ferromagnetic or no coupling between the iron layers, hence it can be assumed that $J(40\,\mathrm{\AA{}}) \approx 0$, showing a rapid reduction in coupling strength with $z$ consistent with the $\nicefrac{1}{z^{3}}$ dependence of the oscillatory interaction. The ferromagnetically coupled 12/10 sample shows that $J(12\ensuremath{\unskip\,\mathrm{\AA{}}})$ is positive, although the magnitude cannot be determined. This too is consistent with an oscillatory $z$ dependence, as illustrated in Figure 5.1. This oscillatory dependence in coupling has been discussed theoretically as arising from RKKY or quantum well mechanisms. The reader is referred to References parkin_91,schilfgaarde_93,bruno_91 for more detailed information.

There is some verification of the results as both the 27/15 and 27/20 samples give consistent values of $J$ within experimental error, as is expected for samples with the same non-magnetic layer thickness.