Continuum Mechanics - Polar Coordinates

Vectors and Tensor Operations in Polar Coordinates

Many simple boundary value problems in solid mechanics (such as those that tend to appear in homework assignments or examinations!) are most conveniently solved using spherical or cylindrical-polar coordinate systems.

The main drawback of using a polar coordinate system is that there is no convenient way to express the various vector and tensor operations using index notation $-$ $-$ everything has to be written out in long-hand. In this section, therefore, we completely abandon index notation $-$ $-$ vector and tensor components are always expressed as matrices.

Spherical-polar coordinates

1.1 Specifying points in spherical-polar coordinates

To specify points in space using spherical-polar coordinates, we first choose two convenient, mutually perpendicular reference directions (i and k in the picture). For example, to specify position on the Earth’s surface, we might choose k to point from the center of the earth towards the North Pole, and choose i to point from the center of the earth towards the intersection of the equator (which has zero degrees latitude) and the Greenwich Meridian (which has zero degrees longitude, by definition).

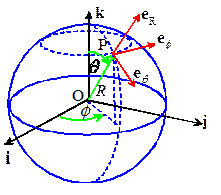
Then, each point P in space is identified by three numbers, $R, θ, ϕ$ $R, θ, ϕ$ shown in the picture above. These are not components of a vector.

In words:

R is the distance of P from the origin

$θ$ $θ$ is the angle between the k direction and OP

$ϕ$ $ϕ$ is the angle between the i direction and the projection of OP onto a plane through O normal to k

By convention, we choose $R \geq 0$ $R \geq 0$ , $0 \leq θ \leq 180^{o}$ $0 \leq θ \leq 180^{o}$ and $0 \leq ϕ \leq 360^{o}$ $0 \leq ϕ \leq 360^{o}$

1.2 Converting between Cartesian and Spherical-Polar representations of points

When we use a Cartesian basis, we identify points in space by specifying the components of their position vector relative to the origin (x,y,z), such that $r = x i + y j + z k$ $r = x i + y j + z k$ When we use a spherical-polar coordinate system, we locate points by specifying their spherical-polar coordinates $R, θ, ϕ$ $R, θ, ϕ$

The formulas below relate the two representations. They are derived using basic trigonometry

$\begin{array}{l} x = R \sin θ \cos ϕ \\ y = R \sin θ \sin ϕ \\ z = R \cos θ \end{array}$ $\begin{array}{l} x = R \sin θ \cos ϕ \\ y = R \sin θ \sin ϕ \\ z = R \cos θ \end{array}$ $\begin{array}{l} R = \sqrt{x^{2} + y^{2} + z^{2}} \\ θ = \cos^{- 1} z / R \\ ϕ = \tan^{- 1} y / x \end{array}$ $\begin{array}{l} R = \sqrt{x^{2} + y^{2} + z^{2}} \\ θ = \cos^{- 1} z / R \\ ϕ = \tan^{- 1} y / x \end{array}$

1.3 Spherical-Polar representation of vectors

When we work with vectors in spherical-polar coordinates, we abandon the {i,j,k} basis. Instead, we specify vectors as components in the ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ basis shown in the figure. For example, an arbitrary vector a is written as $a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ}$ $a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ}$ , where $(a_{R}, a_{θ}, a_{ϕ})$ $(a_{R}, a_{θ}, a_{ϕ})$ denote the components of a.

The basis is different for each point P. In words

$e_{R}$ $e_{R}$ points along OP

$e_{θ}$ $e_{θ}$ is tangent to a line of constant longitude through P

$e_{ϕ}$ $e_{ϕ}$ is tangent to a line of constant latitude through P.

For example if polar-coordinates are used to specify points on the Earth’s surface, you can visualize the basis vectors like this. Suppose you stand at a point P on the Earths surface. Relative to you: $e_{R}$ $e_{R}$ points vertically upwards; $e_{θ}$ $e_{θ}$ points due South; and $e_{ϕ}$ $e_{ϕ}$ points due East. Notice that the basis vectors depend on where you are standing.

You can also visualize the directions as follows. To see the direction of $e_{R}$ $e_{R}$ , keep $θ$ $θ$ and $ϕ$ $ϕ$ fixed, and increase R. P is moving parallel to $e_{R}$ $e_{R}$ . To see the direction of $e_{θ}$ $e_{θ}$ , keep R and $ϕ$ $ϕ$ fixed, and increase $θ$ $θ$ . P now moves parallel to $e_{θ}$ $e_{θ}$ . To see the direction of $e_{ϕ}$ $e_{ϕ}$ , keep R and $θ$ $θ$ fixed, and increase $ϕ$ $ϕ$ . P now moves parallel to $e_{ϕ}$ $e_{ϕ}$ . Mathematically, this concept can be expressed as follows. Let r be the position vector of P. Then

$e_{R} = \frac{1}{| \frac{\partial r}{\partial R} |} \frac{\partial r}{\partial R} e_{θ} = \frac{1}{| \frac{\partial r}{\partial θ} |} \frac{\partial r}{\partial θ} e_{ϕ} = \frac{1}{| \frac{\partial r}{\partial ϕ} |} \frac{\partial r}{\partial ϕ}$ $e_{R} = \frac{1}{| \frac{\partial r}{\partial R} |} \frac{\partial r}{\partial R} e_{θ} = \frac{1}{| \frac{\partial r}{\partial θ} |} \frac{\partial r}{\partial θ} e_{ϕ} = \frac{1}{| \frac{\partial r}{\partial ϕ} |} \frac{\partial r}{\partial ϕ}$

By definition, the `natural basis’ for a coordinate system is the derivative of the position vector with respect to the three scalar coordinates that are used to characterize position in space (see Chapter 10 for a more detailed discussion). The basis vectors for a polar coordinate system are parallel to the natural basis vectors, but are normalized to have unit length. In addition, the natural basis for a polar coordinate system happens to be orthogonal. Consequently, ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ is an orthonormal basis (basis vectors have unit length, are mutually perpendicular and form a right handed triad)

1.4 Converting vectors between Cartesian and Spherical-Polar bases

Let $a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ}$ $a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ}$ be a vector, with components $(a_{R}, a_{θ}, a_{ϕ})$ $(a_{R}, a_{θ}, a_{ϕ})$ in the spherical-polar basis ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ . Let $a_{x}, a_{y}, a_{z}$ $a_{x}, a_{y}, a_{z}$ denote the components of a in the basis {i,j,k}.

The two sets of components are related by

$[\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}] = [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] [\begin{matrix} a_{R} \\ a_{θ} \\ a_{ϕ} \end{matrix}]$ $[\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}] = [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] [\begin{matrix} a_{R} \\ a_{θ} \\ a_{ϕ} \end{matrix}]$

while the inverse relationship is

$[\begin{matrix} a_{R} \\ a_{θ} \\ a_{ϕ} \end{matrix}] = [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] [\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}]$ $[\begin{matrix} a_{R} \\ a_{θ} \\ a_{ϕ} \end{matrix}] = [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] [\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}]$

Observe that the two 3x3 matrices involved in this transformation are transposes (and inverses) of one another. The transformation matrix is therefore orthogonal, satisfying $[Q] {[Q]}^{T} = [I]$ $[Q] {[Q]}^{T} = [I]$ , where $[I]$ $[I]$ denotes the 3x3 identity matrix.

Derivation: It is easiest to do the transformation by expressing each basis vector ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ as components in {i,j,k}, and then substituting. To do this, recall that $r = x i + y j + z k$ $r = x i + y j + z k$ , recall also the conversion

$x = R \sin θ \cos ϕ y = R \sin θ \sin ϕ z = R \cos θ$ $x = R \sin θ \cos ϕ y = R \sin θ \sin ϕ z = R \cos θ$

and finally recall that by definition

Hence, substituting for x,y,z and differentiating

$\begin{array}{l} r = R \sin θ \cos ϕ i + R \sin θ \sin ϕ j + R \cos θ k \\ \Rightarrow \frac{\partial r}{\partial R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k \end{array}$ $\begin{array}{l} r = R \sin θ \cos ϕ i + R \sin θ \sin ϕ j + R \cos θ k \\ \Rightarrow \frac{\partial r}{\partial R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k \end{array}$

Conveniently we find that $| \frac{\partial r}{\partial R} | = 1$ $| \frac{\partial r}{\partial R} | = 1$ . Therefore

$e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k$ $e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k$

Similarly

$\begin{array}{l} \frac{\partial r}{\partial θ} = R \cos θ \cos ϕ i + R \cos θ \sin ϕ j - R \sin θ k \\ \frac{\partial r}{\partial ϕ} = - R \sin θ \sin ϕ i + R \sin θ \cos ϕ j \end{array}$ $\begin{array}{l} \frac{\partial r}{\partial θ} = R \cos θ \cos ϕ i + R \cos θ \sin ϕ j - R \sin θ k \\ \frac{\partial r}{\partial ϕ} = - R \sin θ \sin ϕ i + R \sin θ \cos ϕ j \end{array}$

while $| \frac{\partial r}{\partial θ} | = R$ $| \frac{\partial r}{\partial θ} | = R$ , $| \frac{\partial r}{\partial ϕ} | = R \sin θ$ $| \frac{\partial r}{\partial ϕ} | = R \sin θ$ so that

$e_{θ} = \cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k$ $e_{θ} = \cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k$ $e_{ϕ} = - \sin ϕ i + \cos ϕ j$ $e_{ϕ} = - \sin ϕ i + \cos ϕ j$

Finally, substituting

$\begin{array}{l} a = a_{R} [\sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k] \\ + a_{θ} [\cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k] \\ + a_{ϕ} [- \sin ϕ i + \cos ϕ j] \end{array}$ $\begin{array}{l} a = a_{R} [\sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k] \\ + a_{θ} [\cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k] \\ + a_{ϕ} [- \sin ϕ i + \cos ϕ j] \end{array}$

Collecting terms in i, j and k, we see that

$\begin{array}{l} a_{x} = \sin θ \cos ϕ a_{R} + \cos θ \cos ϕ a_{θ} - \sin ϕ a_{ϕ} \\ a_{y} = \sin θ \sin ϕ a_{R} + \cos θ \sin ϕ a_{θ} + \cos ϕ a_{ϕ} \\ a_{z} = \cos θ a_{R} - \sin θ a_{θ} \end{array}$ $\begin{array}{l} a_{x} = \sin θ \cos ϕ a_{R} + \cos θ \cos ϕ a_{θ} - \sin ϕ a_{ϕ} \\ a_{y} = \sin θ \sin ϕ a_{R} + \cos θ \sin ϕ a_{θ} + \cos ϕ a_{ϕ} \\ a_{z} = \cos θ a_{R} - \sin θ a_{θ} \end{array}$

This is the result stated.

To show the inverse result, start by noting that

$\begin{array}{l} a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ} = a_{x} i + a_{y} j + a_{z} k \\ \Rightarrow a \cdot e_{R} = a_{R} = a_{x} i \cdot e_{R} + a_{y} j \cdot e_{R} + a_{z} k \cdot e_{R} \end{array}$ $\begin{array}{l} a = a_{R} e_{R} + a_{θ} e_{θ} + a_{ϕ} e_{ϕ} = a_{x} i + a_{y} j + a_{z} k \\ \Rightarrow a \cdot e_{R} = a_{R} = a_{x} i \cdot e_{R} + a_{y} j \cdot e_{R} + a_{z} k \cdot e_{R} \end{array}$

(where we have used $e_{θ} \cdot e_{R} = e_{ϕ} \cdot e_{R} = 0$ $e_{θ} \cdot e_{R} = e_{ϕ} \cdot e_{R} = 0$ ). Recall that

$\begin{array}{l} e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k \\ \Rightarrow i \cdot e_{R} = \sin θ \cos ϕ j \cdot e_{R} = \sin θ \sin ϕ k \cdot e_{R} = \cos θ \end{array}$ $\begin{array}{l} e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k \\ \Rightarrow i \cdot e_{R} = \sin θ \cos ϕ j \cdot e_{R} = \sin θ \sin ϕ k \cdot e_{R} = \cos θ \end{array}$

Substituting, we get

$a_{R} = \sin θ \cos ϕ a_{x} + \sin θ \sin ϕ a_{y} + \cos θ a_{z}$ $a_{R} = \sin θ \cos ϕ a_{x} + \sin θ \sin ϕ a_{y} + \cos θ a_{z}$

Proceeding in exactly the same way for the other two components gives the remaining expressions

$\begin{array}{l} a_{θ} = \cos θ \cos ϕ a_{x} + \cos θ \sin ϕ a_{y} - \sin θ a_{z} \\ a_{ϕ} = - \sin ϕ a_{x} + \cos ϕ a_{y} \end{array}$ $\begin{array}{l} a_{θ} = \cos θ \cos ϕ a_{x} + \cos θ \sin ϕ a_{y} - \sin θ a_{z} \\ a_{ϕ} = - \sin ϕ a_{x} + \cos ϕ a_{y} \end{array}$

Re-writing the last three equations in matrix form gives the result stated.

1.5 Spherical-Polar representation of tensors

The triad of vectors ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ is an orthonormal basis (i.e. the three basis vectors have unit length, and are mutually perpendicular). Consequently, tensors can be represented as components in this basis in exactly the same way as for a fixed Cartesian basis ${e_{1}, e_{2}, e_{3}}$ ${e_{1}, e_{2}, e_{3}}$ . In particular, a general second order tensor S can be represented as a 3x3 matrix

$S \equiv [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}]$ $S \equiv [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}]$

You can think of $S_{R R}$ $S_{R R}$ as being equivalent to $S_{11}$ $S_{11}$ , $S_{R θ}$ $S_{R θ}$ as $S_{12}$ $S_{12}$ , and so on. All tensor operations such as addition, multiplication by a vector, tensor products, etc can be expressed in terms of the corresponding operations on this matrix, as discussed in Section B2 of Appendix B.

The component representation of a tensor can also be expressed in dyadic form as

$\begin{array}{l} S = S_{R R} e_{R} \otimes e_{R} + S_{R θ} e_{R} \otimes e_{θ} + S_{R ϕ} e_{R} \otimes e_{ϕ} \\ + S_{θ R} e_{θ} \otimes e_{R} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ ϕ} e_{θ} \otimes e_{ϕ} \\ + S_{ϕ R} e_{ϕ} \otimes e_{R} + S_{ϕ θ} e_{ϕ} \otimes e_{θ} + S_{ϕ ϕ} e_{ϕ} \otimes e_{ϕ} \end{array}$ $\begin{array}{l} S = S_{R R} e_{R} \otimes e_{R} + S_{R θ} e_{R} \otimes e_{θ} + S_{R ϕ} e_{R} \otimes e_{ϕ} \\ + S_{θ R} e_{θ} \otimes e_{R} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ ϕ} e_{θ} \otimes e_{ϕ} \\ + S_{ϕ R} e_{ϕ} \otimes e_{R} + S_{ϕ θ} e_{ϕ} \otimes e_{θ} + S_{ϕ ϕ} e_{ϕ} \otimes e_{ϕ} \end{array}$

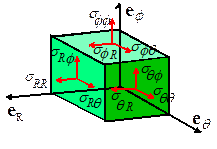Furthermore, the physical significance of the components can be interpreted in exactly the same way as for tensor components in a Cartesian basis. For example, the spherical-polar coordinate representation for the Cauchy stress tensor has the form

$σ \equiv [\begin{matrix} σ_{R R} & σ_{R θ} & σ_{R ϕ} \\ σ_{θ R} & σ_{θ θ} & σ_{θ ϕ} \\ σ_{ϕ R} & σ_{ϕ θ} & σ_{ϕ ϕ} \end{matrix}]$ $σ \equiv [\begin{matrix} σ_{R R} & σ_{R θ} & σ_{R ϕ} \\ σ_{θ R} & σ_{θ θ} & σ_{θ ϕ} \\ σ_{ϕ R} & σ_{ϕ θ} & σ_{ϕ ϕ} \end{matrix}]$

The component $σ_{θ R}$ $σ_{θ R}$ represents the traction component in direction $e_{R}$ $e_{R}$ acting on an internal material plane with normal $e_{θ}$ $e_{θ}$ , and so on. Of course, the Cauchy stress tensor is symmetric, with $σ_{θ R} = σ_{R θ}$ $σ_{θ R} = σ_{R θ}$

1.6 Constitutive equations in spherical-polar coordinates

The constitutive equations listed in Chapter 3 all relate some measure of stress in the solid (expressed as a tensor) to some measure of local internal deformation (deformation gradient, Eulerian strain, rate of deformation tensor, etc), also expressed as a tensor. The constitutive equations can be used without modification in spherical-polar coordinates, as long as the matrices of Cartesian components of the various tensors are replaced by their equivalent matrices in spherical-polar coordinates.

For example, the stress-strain relations for an isotropic, linear elastic material in spherical-polar coordinates read

$[\begin{matrix} ε_{R R} \\ ε_{θ θ} \\ ε_{ϕ ϕ} \\ 2 ε_{θ ϕ} \\ 2 ε_{R ϕ} \\ 2 ε_{R θ} \end{matrix}] = \frac{1}{E} [\begin{matrix} 1 & - ν & - ν & 0 & 0 & 0 \\ - ν & 1 & - ν & 0 & 0 & 0 \\ - ν & - ν & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 (1 + ν) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 (1 + ν) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 (1 + ν) \end{matrix}] [\begin{matrix} σ_{R R} \\ σ_{θ θ} \\ σ_{ϕ ϕ} \\ σ_{θ ϕ} \\ σ_{R ϕ} \\ σ_{R θ} \end{matrix}] + α Δ T [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix}]$ $[\begin{matrix} ε_{R R} \\ ε_{θ θ} \\ ε_{ϕ ϕ} \\ 2 ε_{θ ϕ} \\ 2 ε_{R ϕ} \\ 2 ε_{R θ} \end{matrix}] = \frac{1}{E} [\begin{matrix} 1 & - ν & - ν & 0 & 0 & 0 \\ - ν & 1 & - ν & 0 & 0 & 0 \\ - ν & - ν & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 (1 + ν) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 (1 + ν) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 (1 + ν) \end{matrix}] [\begin{matrix} σ_{R R} \\ σ_{θ θ} \\ σ_{ϕ ϕ} \\ σ_{θ ϕ} \\ σ_{R ϕ} \\ σ_{R θ} \end{matrix}] + α Δ T [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix}]$

HEALTH WARNING: If you are solving a problem involving anisotropic materials using spherical-polar coordinates, it is important to remember that the orientation of the basis vectors ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ vary with position. For example, for an anisotropic, linear elastic solid you could write the constitutive equation as

$\begin{array}{l} σ = C (ε - α Δ T) \\ σ = [\begin{matrix} σ_{R R} \\ σ_{θ θ} \\ σ_{ϕ ϕ} \\ σ_{θ ϕ} \\ σ_{R ϕ} \\ σ_{R θ} \end{matrix}] C = [\begin{matrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} \\ c_{12} & c_{22} & c_{23} & c_{24} & c_{25} & c_{26} \\ c_{13} & c_{23} & c_{33} & c_{34} & c_{35} & c_{36} \\ c_{14} & c_{24} & c_{34} & c_{44} & c_{45} & c_{46} \\ c_{15} & c_{25} & c_{35} & c_{45} & c_{55} & c_{56} \\ c_{16} & c_{26} & c_{36} & c_{46} & c_{56} & c_{66} \end{matrix}] ε = [\begin{matrix} ε_{R R} \\ ε_{θ θ} \\ ε_{ϕ ϕ} \\ 2 ε_{θ ϕ} \\ 2 ε_{R ϕ} \\ 2 ε_{R θ} \end{matrix}] α = [\begin{matrix} α_{R R} \\ α_{θ θ} \\ α_{ϕ ϕ} \\ 2 α_{θ ϕ} \\ 2 α_{R ϕ} \\ 2 α_{R θ} \end{matrix}] \end{array}$ $\begin{array}{l} σ = C (ε - α Δ T) \\ σ = [\begin{matrix} σ_{R R} \\ σ_{θ θ} \\ σ_{ϕ ϕ} \\ σ_{θ ϕ} \\ σ_{R ϕ} \\ σ_{R θ} \end{matrix}] C = [\begin{matrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} \\ c_{12} & c_{22} & c_{23} & c_{24} & c_{25} & c_{26} \\ c_{13} & c_{23} & c_{33} & c_{34} & c_{35} & c_{36} \\ c_{14} & c_{24} & c_{34} & c_{44} & c_{45} & c_{46} \\ c_{15} & c_{25} & c_{35} & c_{45} & c_{55} & c_{56} \\ c_{16} & c_{26} & c_{36} & c_{46} & c_{56} & c_{66} \end{matrix}] ε = [\begin{matrix} ε_{R R} \\ ε_{θ θ} \\ ε_{ϕ ϕ} \\ 2 ε_{θ ϕ} \\ 2 ε_{R ϕ} \\ 2 ε_{R θ} \end{matrix}] α = [\begin{matrix} α_{R R} \\ α_{θ θ} \\ α_{ϕ ϕ} \\ 2 α_{θ ϕ} \\ 2 α_{R ϕ} \\ 2 α_{R θ} \end{matrix}] \end{array}$

however, the elastic constants $c_{11}, c_{12}, ...$ $c_{11}, c_{12}, ...$ would need to be represent the material properties in the basis ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ , and would therefore be functions of position (you would have to calculate them using the lengthy basis change formulas listed in Section 3.2.11). In practice the results are so complicated that there would be very little advantage in working with a spherical-polar coordinate system in this situation.

1.7 Converting tensors between Cartesian and Spherical-Polar bases

Let S be a tensor, with components

$S \equiv [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}]$ $S \equiv [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}]$

in the spherical-polar basis ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ and the Cartesian basis {i,j,k}, respectively. The two sets of components are related by

$\begin{array}{l} [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] = \\ [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] \end{array}$ $\begin{array}{l} [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] = \\ [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] \end{array}$

$\begin{array}{l} [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] = \\ [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] \end{array}$ $\begin{array}{l} [\begin{matrix} S_{R R} & S_{R θ} & S_{R ϕ} \\ S_{θ R} & S_{θ θ} & S_{θ ϕ} \\ S_{ϕ R} & S_{ϕ θ} & S_{ϕ ϕ} \end{matrix}] = \\ [\begin{matrix} \sin θ \cos ϕ & \sin θ \sin ϕ & \cos θ \\ \cos θ \cos ϕ & \cos θ \sin ϕ & - \sin θ \\ - \sin ϕ & \cos ϕ & 0 \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] [\begin{matrix} \sin θ \cos ϕ & \cos θ \cos ϕ & - \sin ϕ \\ \sin θ \sin ϕ & \cos θ \sin ϕ & \cos ϕ \\ \cos θ & - \sin θ & 0 \end{matrix}] \end{array}$

These results follow immediately from the general basis change formulas for tensors .

1.8 Vector Calculus using Spherical-Polar Coordinates

Calculating derivatives of scalar, vector and tensor functions of position in spherical-polar coordinates is complicated by the fact that the basis vectors are functions of position. The results can be expressed in a compact form by defining the gradient operator, which, in spherical-polar coordinates, has the representation

$\nabla \equiv (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ})$ $\nabla \equiv (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ})$

In addition, the derivatives of the basis vectors are

$\begin{array}{l} \frac{\partial e_{R}}{\partial R} = \frac{\partial e_{θ}}{\partial R} = \frac{\partial e_{ϕ}}{\partial R} = 0 \frac{\partial e_{R}}{\partial θ} = e_{θ} \frac{\partial e_{θ}}{\partial θ} = - e_{R} \frac{\partial e_{ϕ}}{\partial θ} = 0 \\ \frac{\partial e_{R}}{\partial ϕ} = \sin θ e_{ϕ} \frac{\partial e_{θ}}{\partial ϕ} = \cos θ e_{ϕ} \frac{\partial e_{ϕ}}{\partial ϕ} = - \sin θ e_{R} - \cos θ e_{θ} \end{array}$ $\begin{array}{l} \frac{\partial e_{R}}{\partial R} = \frac{\partial e_{θ}}{\partial R} = \frac{\partial e_{ϕ}}{\partial R} = 0 \frac{\partial e_{R}}{\partial θ} = e_{θ} \frac{\partial e_{θ}}{\partial θ} = - e_{R} \frac{\partial e_{ϕ}}{\partial θ} = 0 \\ \frac{\partial e_{R}}{\partial ϕ} = \sin θ e_{ϕ} \frac{\partial e_{θ}}{\partial ϕ} = \cos θ e_{ϕ} \frac{\partial e_{ϕ}}{\partial ϕ} = - \sin θ e_{R} - \cos θ e_{θ} \end{array}$

You can derive these formulas by differentiating the expressions for the basis vectors in terms of {i,j,k}

$e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k$ $e_{R} = \sin θ \cos ϕ i + \sin θ \sin ϕ j + \cos θ k$ $e_{θ} = \cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k$ $e_{θ} = \cos θ \cos ϕ i + \cos θ \sin ϕ j - \sin θ k$ $e_{ϕ} = - \sin ϕ i + \cos ϕ j$ $e_{ϕ} = - \sin ϕ i + \cos ϕ j$

and evaluating the various derivatives. When differentiating, note that {i,j,k} are fixed, so their derivatives are zero. The details are left as an exercise.

The various derivatives of scalars, vectors and tensors can be expressed using operator notation as follows.

Gradient of a scalar function: Let $f (R, θ, ϕ)$ $f (R, θ, ϕ)$ denote a scalar function of position. The gradient of f is denoted by

$\nabla f = f (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) = e_{R} \frac{\partial f}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial f}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial f}{\partial ϕ}$ $\nabla f = f (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) = e_{R} \frac{\partial f}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial f}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial f}{\partial ϕ}$

Alternatively, in matrix form

$\nabla f = {[\frac{\partial f}{\partial R}, \frac{1}{R} \frac{\partial f}{\partial θ}, \frac{1}{R \sin θ} \frac{\partial f}{\partial ϕ}]}^{T}$ $\nabla f = {[\frac{\partial f}{\partial R}, \frac{1}{R} \frac{\partial f}{\partial θ}, \frac{1}{R \sin θ} \frac{\partial f}{\partial ϕ}]}^{T}$

Gradient of a vector function Let $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ be a vector function of position. The gradient of v is a tensor, which can be represented as a dyadic product of the vector with the gradient operator as

$v \otimes \nabla = (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}) \otimes (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ})$ $v \otimes \nabla = (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}) \otimes (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ})$

The dyadic product can be expanded $-$ $-$ but when evaluating the derivatives it is important to recall that the basis vectors are functions of the coordinates $(R, θ, ϕ)$ $(R, θ, ϕ)$ and consequently their derivatives do not vanish. For example

$\frac{1}{R} \frac{\partial}{\partial θ} (v_{R} e_{R}) \otimes e_{θ} = \frac{1}{R} \frac{\partial v_{R}}{\partial θ} e_{R} \otimes e_{θ} + \frac{v_{R}}{R} \frac{\partial e_{R}}{\partial θ} \otimes e_{θ} = \frac{1}{R} \frac{\partial v_{R}}{\partial θ} e_{R} \otimes e_{θ} + \frac{v_{R}}{R} e_{θ} \otimes e_{θ}$ $\frac{1}{R} \frac{\partial}{\partial θ} (v_{R} e_{R}) \otimes e_{θ} = \frac{1}{R} \frac{\partial v_{R}}{\partial θ} e_{R} \otimes e_{θ} + \frac{v_{R}}{R} \frac{\partial e_{R}}{\partial θ} \otimes e_{θ} = \frac{1}{R} \frac{\partial v_{R}}{\partial θ} e_{R} \otimes e_{θ} + \frac{v_{R}}{R} e_{θ} \otimes e_{θ}$

Verify for yourself that the matrix representing the components of the gradient of a vector is

$v \otimes \nabla \equiv [\begin{matrix} \frac{\partial v_{R}}{\partial R} & \frac{1}{R} \frac{\partial v_{R}}{\partial θ} - \frac{v_{θ}}{R} & \frac{1}{R \sin θ} \frac{\partial v_{R}}{\partial ϕ} - \frac{v_{ϕ}}{R} \\ \frac{\partial v_{θ}}{\partial R} & \frac{1}{R} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{R}}{R} & \frac{1}{R \sin θ} \frac{\partial v_{θ}}{\partial ϕ} - \cot θ \frac{v_{ϕ}}{R} \\ \frac{\partial v_{ϕ}}{\partial R} & \frac{1}{R} \frac{\partial v_{ϕ}}{\partial θ} & \frac{1}{R \sin θ} \frac{\partial v_{ϕ}}{\partial ϕ} + \cot θ \frac{v_{θ}}{R} + \frac{v_{R}}{R} \end{matrix}]$ $v \otimes \nabla \equiv [\begin{matrix} \frac{\partial v_{R}}{\partial R} & \frac{1}{R} \frac{\partial v_{R}}{\partial θ} - \frac{v_{θ}}{R} & \frac{1}{R \sin θ} \frac{\partial v_{R}}{\partial ϕ} - \frac{v_{ϕ}}{R} \\ \frac{\partial v_{θ}}{\partial R} & \frac{1}{R} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{R}}{R} & \frac{1}{R \sin θ} \frac{\partial v_{θ}}{\partial ϕ} - \cot θ \frac{v_{ϕ}}{R} \\ \frac{\partial v_{ϕ}}{\partial R} & \frac{1}{R} \frac{\partial v_{ϕ}}{\partial θ} & \frac{1}{R \sin θ} \frac{\partial v_{ϕ}}{\partial ϕ} + \cot θ \frac{v_{θ}}{R} + \frac{v_{R}}{R} \end{matrix}]$

Divergence of a vector function Let $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ be a vector function of position. The divergence of v is a scalar, which can be represented as a dot product of the vector with the gradient operator as

$\nabla \cdot v = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \cdot (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ})$ $\nabla \cdot v = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \cdot (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ})$

Again, when expanding the dot product, it is important to remember to differentiate the basis vectors. Alternatively, the divergence can be expressed as $trace (v \otimes \nabla)$ $trace (v \otimes \nabla)$ , which immediately gives

$\nabla \cdot v \equiv \frac{\partial v_{R}}{\partial R} + 2 \frac{v_{R}}{R} + \frac{1}{R} \frac{\partial v_{θ}}{\partial θ} + \frac{1}{R \sin θ} \frac{\partial v_{ϕ}}{\partial ϕ} + \cot θ \frac{v_{θ}}{R}$ $\nabla \cdot v \equiv \frac{\partial v_{R}}{\partial R} + 2 \frac{v_{R}}{R} + \frac{1}{R} \frac{\partial v_{θ}}{\partial θ} + \frac{1}{R \sin θ} \frac{\partial v_{ϕ}}{\partial ϕ} + \cot θ \frac{v_{θ}}{R}$

Curl of a vector function Let $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ}$ be a vector function of position. The curl of v is a vector, which can be represented as a cross product of the vector with the gradient operator as

$\nabla \times v = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \times (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ})$ $\nabla \times v = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \times (v_{R} e_{R} + v_{θ} e_{θ} + v_{ϕ} e_{ϕ})$

The curl rarely appears in solid mechanics so the components will not be expanded in full

Divergence of a tensor function. Let $S$ $S$ be a tensor, with dyadic representation

The divergence of S is a vector, which can be represented as

$\nabla \cdot S = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \cdot (\begin{matrix} S_{R R} e_{R} \otimes e_{R} + S_{R θ} e_{R} \otimes e_{θ} + S_{R ϕ} e_{R} \otimes e_{ϕ} \\ + S_{θ R} e_{θ} \otimes e_{R} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ ϕ} e_{θ} \otimes e_{ϕ} \\ + S_{ϕ R} e_{ϕ} \otimes e_{R} + S_{ϕ θ} e_{ϕ} \otimes e_{θ} + S_{ϕ ϕ} e_{ϕ} \otimes e_{ϕ} \end{matrix})$ $\nabla \cdot S = (e_{R} \frac{\partial}{\partial R} + e_{θ} \frac{1}{R} \frac{\partial}{\partial θ} + e_{ϕ} \frac{1}{R \sin θ} \frac{\partial}{\partial ϕ}) \cdot (\begin{matrix} S_{R R} e_{R} \otimes e_{R} + S_{R θ} e_{R} \otimes e_{θ} + S_{R ϕ} e_{R} \otimes e_{ϕ} \\ + S_{θ R} e_{θ} \otimes e_{R} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ ϕ} e_{θ} \otimes e_{ϕ} \\ + S_{ϕ R} e_{ϕ} \otimes e_{R} + S_{ϕ θ} e_{ϕ} \otimes e_{θ} + S_{ϕ ϕ} e_{ϕ} \otimes e_{ϕ} \end{matrix})$

Evaluating the components of the divergence is an extremely tedious operation, because each of the basis vectors in the dyadic representation of S must be differentiated, in addition to the components themselves. The final result (expressed as a column vector) is

$\nabla \cdot S \equiv [\begin{matrix} \frac{\partial S_{R R}}{\partial R} + 2 \frac{S_{R R}}{R} + \frac{1}{R} \frac{\partial S_{θ R}}{\partial θ} + \cot θ \frac{S_{θ R}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ R}}{\partial ϕ} - \frac{1}{R} (S_{θ θ} + S_{ϕ ϕ}) \\ \frac{\partial S_{R θ}}{\partial R} + 2 \frac{S_{R θ}}{R} + \frac{1}{R} \frac{\partial S_{θ θ}}{\partial θ} + \cot θ \frac{S_{θ θ}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ θ}}{\partial ϕ} + \frac{S_{θ R}}{R} - \cot θ \frac{S_{ϕ ϕ}}{R} \\ \frac{\partial S_{R ϕ}}{\partial R} + 2 \frac{S_{R ϕ}}{R} + \frac{\sin θ}{R} \frac{\partial S_{θ ϕ}}{\partial θ} + \cos θ \frac{S_{θ ϕ}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ ϕ}}{\partial ϕ} + \frac{1}{R} (S_{ϕ R} + S_{ϕ θ}) \end{matrix}]$ $\nabla \cdot S \equiv [\begin{matrix} \frac{\partial S_{R R}}{\partial R} + 2 \frac{S_{R R}}{R} + \frac{1}{R} \frac{\partial S_{θ R}}{\partial θ} + \cot θ \frac{S_{θ R}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ R}}{\partial ϕ} - \frac{1}{R} (S_{θ θ} + S_{ϕ ϕ}) \\ \frac{\partial S_{R θ}}{\partial R} + 2 \frac{S_{R θ}}{R} + \frac{1}{R} \frac{\partial S_{θ θ}}{\partial θ} + \cot θ \frac{S_{θ θ}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ θ}}{\partial ϕ} + \frac{S_{θ R}}{R} - \cot θ \frac{S_{ϕ ϕ}}{R} \\ \frac{\partial S_{R ϕ}}{\partial R} + 2 \frac{S_{R ϕ}}{R} + \frac{\sin θ}{R} \frac{\partial S_{θ ϕ}}{\partial θ} + \cos θ \frac{S_{θ ϕ}}{R} + \frac{1}{R \sin θ} \frac{\partial S_{ϕ ϕ}}{\partial ϕ} + \frac{1}{R} (S_{ϕ R} + S_{ϕ θ}) \end{matrix}]$

2: Cylindrical-polar coordinates

2.1 Specifying points in space using in cylindrical-polar coordinates

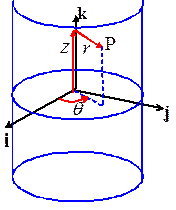
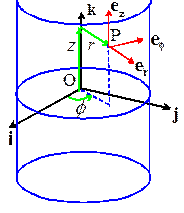
To specify the location of a point in cylindrical-polar coordinates, we choose an origin at some point on the axis of the cylinder, select a unit vector k to be parallel to the axis of the cylinder, and choose a convenient direction for the basis vector i, as shown in the picture. We then use the three numbers $r, θ, z$ $r, θ, z$ to locate a point inside the cylinder, as shown in the picture. These are not components of a vector.

In words

r is the radial distance of P from the axis of the cylinder

$ϕ$ $ϕ$ is the angle between the i direction and the projection of OP onto the i,j plane

z is the length of the projection of OP on the axis of the cylinder.

By convention r>0 and $0 \leq θ \leq 360^{o}$ $0 \leq θ \leq 360^{o}$

2.2 Converting between cylindrical polar and rectangular cartesian coordinates

The formulas below relate the two representations. They are derived using basic trigonometry

$\begin{array}{l} x = r \cos θ \\ y = r \sin θ \\ z = z \end{array}$ $\begin{array}{l} x = r \cos θ \\ y = r \sin θ \\ z = z \end{array}$ $\begin{array}{l} r = \sqrt{x^{2} + y^{2}} \\ θ = \tan^{- 1} y / x \\ z = z \end{array}$ $\begin{array}{l} r = \sqrt{x^{2} + y^{2}} \\ θ = \tan^{- 1} y / x \\ z = z \end{array}$

2.3 Cylindrical-polar representation of vectors

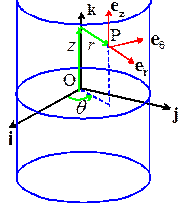
When we work with vectors in spherical-polar coordinates, we specify vectors as components in the ${e_{r}, e_{θ}, e_{z}}$ ${e_{r}, e_{θ}, e_{z}}$ basis shown in the figure. For example, an arbitrary vector a is written as $a = a_{r} e_{r} + a_{θ} e_{θ} + a_{z} e_{z}$ $a = a_{r} e_{r} + a_{θ} e_{θ} + a_{z} e_{z}$ , where $(a_{r}, a_{θ}, a_{z})$ $(a_{r}, a_{θ}, a_{z})$ denote the components of a.

The basis vectors are selected as follows

$e_{r}$ $e_{r}$ is a unit vector normal to the cylinder at P

$e_{θ}$ $e_{θ}$ is a unit vector circumferential to the cylinder at P, chosen to make ${e_{r}, e_{θ}, e_{z}}$ ${e_{r}, e_{θ}, e_{z}}$ a right handed triad

$e_{z}$ $e_{z}$ is parallel to the k vector.

You will see that the position vector of point P would be expressed as

$r = r e_{r} + z e_{z} = r \cos θ i + r \sin θ j + z k$ $r = r e_{r} + z e_{z} = r \cos θ i + r \sin θ j + z k$

Note also that the basis vectors are intentionally chosen to satisfy

$e_{r} = \frac{1}{| \frac{\partial r}{\partial r} |} \frac{\partial r}{\partial r} e_{ϕ} = \frac{1}{| \frac{\partial r}{\partial θ} |} \frac{\partial r}{\partial θ} e_{z} = \frac{1}{| \frac{\partial r}{\partial z} |} \frac{\partial r}{\partial z}$ $e_{r} = \frac{1}{| \frac{\partial r}{\partial r} |} \frac{\partial r}{\partial r} e_{ϕ} = \frac{1}{| \frac{\partial r}{\partial θ} |} \frac{\partial r}{\partial θ} e_{z} = \frac{1}{| \frac{\partial r}{\partial z} |} \frac{\partial r}{\partial z}$

The basis vectors have unit length, are mutually perpendicular, and form a right handed triad and therefore ${e_{r}, e_{θ}, e_{z}}$ ${e_{r}, e_{θ}, e_{z}}$ is an orthonormal basis. The basis vectors are parallel to (but not equivalent to) the natural basis vectors for a cylindrical polar coordinate system (see Chapter 10 for a more detailed discussion).

2.4 Converting vectors between Cylindrical and Cartesian bases

Let $a = a_{r} e_{r} + a_{θ} e_{θ} + a_{z} e_{z}$ $a = a_{r} e_{r} + a_{θ} e_{θ} + a_{z} e_{z}$ be a vector, with components $(a_{r}, a_{θ}, a_{z})$ $(a_{r}, a_{θ}, a_{z})$ in the spherical-polar basis ${e_{R}, e_{θ}, e_{ϕ}}$ ${e_{R}, e_{θ}, e_{ϕ}}$ . Let $a_{x}, a_{y}, a_{z}$ $a_{x}, a_{y}, a_{z}$ denote the components of a in the basis {i,j,k}.

The two sets of components are related by

$[\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}] = [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} a_{r} \\ a_{θ} \\ a_{z} \end{matrix}]$ $[\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}] = [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} a_{r} \\ a_{θ} \\ a_{z} \end{matrix}]$ $[\begin{matrix} a_{r} \\ a_{θ} \\ a_{z} \end{matrix}] = [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}]$ $[\begin{matrix} a_{r} \\ a_{θ} \\ a_{z} \end{matrix}] = [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}]$

The derivation of these results follows the procedure outlined in E.1.4 exactly, and is left as an exercise.

2.5 Cylindrical-Polar representation of tensors

The triad of vectors ${e_{r}, e_{θ}, e_{z}}$ ${e_{r}, e_{θ}, e_{z}}$ is an orthonormal basis (i.e. the three basis vectors have unit length, and are mutually perpendicular). Consequently, tensors can be represented as components in this basis in exactly the same way as for a fixed Cartesian basis ${e_{1}, e_{2}, e_{3}}$ ${e_{1}, e_{2}, e_{3}}$ . In particular, a general second order tensor S can be represented as a 3x3 matrix

$S \equiv [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}]$ $S \equiv [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}]$

You can think of $S_{r r}$ $S_{r r}$ as being equivalent to $S_{11}$ $S_{11}$ , $S_{r θ}$ $S_{r θ}$ as $S_{12}$ $S_{12}$ , and so on. All tensor operations such as addition, multiplication by a vector, tensor products, etc can be expressed in terms of the corresponding operations on this matrix, as discussed in Section B2 of Appendix B.

The component representation of a tensor can also be expressed in dyadic form as

$\begin{array}{l} S = S_{r r} e_{r} \otimes e_{r} + S_{r θ} e_{r} \otimes e_{θ} + S_{r z} e_{r} \otimes e_{z} \\ + S_{θ r} e_{θ} \otimes e_{r} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ z} e_{θ} \otimes e_{z} \\ + S_{z r} e_{z} \otimes e_{r} + S_{z θ} e_{z} \otimes e_{θ} + S_{z z} e_{z} \otimes e_{z} \end{array}$ $\begin{array}{l} S = S_{r r} e_{r} \otimes e_{r} + S_{r θ} e_{r} \otimes e_{θ} + S_{r z} e_{r} \otimes e_{z} \\ + S_{θ r} e_{θ} \otimes e_{r} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ z} e_{θ} \otimes e_{z} \\ + S_{z r} e_{z} \otimes e_{r} + S_{z θ} e_{z} \otimes e_{θ} + S_{z z} e_{z} \otimes e_{z} \end{array}$

The remarks in Section E.1.5 regarding the physical significance of tensor components also applies to tensor components in cylindrical-polar coordinates.

2.6 Constitutive equations in cylindrical-polar coordinates

The constitutive equations listed in Chapter 3 all relate some measure of stress in the solid (expressed as a tensor) to some measure of local internal deformation (deformation gradient, Eulerian strain, rate of deformation tensor, etc), also expressed as a tensor. The constitutive equations can be used without modification in cylindrical-polar coordinates, as long as the matrices of Cartesian components of the various tensors are replaced by their equivalent matrices in spherical-polar coordinates.

For example, the stress-strain relations for an isotropic, linear elastic material in cylindrical-polar coordinates read

$[\begin{matrix} ε_{r r} \\ ε_{θ θ} \\ ε_{z z} \\ 2 ε_{θ z} \\ 2 ε_{r z} \\ 2 ε_{r θ} \end{matrix}] = \frac{1}{E} [\begin{matrix} 1 & - ν & - ν & 0 & 0 & 0 \\ - ν & 1 & - ν & 0 & 0 & 0 \\ - ν & - ν & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 (1 + ν) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 (1 + ν) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 (1 + ν) \end{matrix}] [\begin{matrix} σ_{r r} \\ σ_{θ θ} \\ σ_{z z} \\ σ_{θ z} \\ σ_{r z} \\ σ_{r θ} \end{matrix}] + α Δ T [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix}]$ $[\begin{matrix} ε_{r r} \\ ε_{θ θ} \\ ε_{z z} \\ 2 ε_{θ z} \\ 2 ε_{r z} \\ 2 ε_{r θ} \end{matrix}] = \frac{1}{E} [\begin{matrix} 1 & - ν & - ν & 0 & 0 & 0 \\ - ν & 1 & - ν & 0 & 0 & 0 \\ - ν & - ν & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 (1 + ν) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 (1 + ν) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 (1 + ν) \end{matrix}] [\begin{matrix} σ_{r r} \\ σ_{θ θ} \\ σ_{z z} \\ σ_{θ z} \\ σ_{r z} \\ σ_{r θ} \end{matrix}] + α Δ T [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix}]$

The cautionary remarks regarding anisotropic materials in E.1.6 also applies to cylindrical-polar coordinate systems.

2.7 Converting tensors between Cartesian and Spherical-Polar bases

Let S be a tensor, with components

$S \equiv [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] \equiv [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}]$ $S \equiv [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] \equiv [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}]$

in the cylindrical-polar basis ${e_{r}, e_{θ}, e_{z}}$ ${e_{r}, e_{θ}, e_{z}}$ and the Cartesian basis {i,j,k}, respectively. The two sets of components are related by

$[\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] = [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}]$ $[\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] = [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}]$

$[\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] = [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}]$ $[\begin{matrix} S_{r r} & S_{r θ} & S_{r z} \\ S_{θ r} & S_{θ θ} & S_{θ z} \\ S_{z r} & S_{z θ} & S_{z z} \end{matrix}] = [\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} S_{x x} & S_{x y} & S_{x z} \\ S_{y x} & S_{y y} & S_{y z} \\ S_{z x} & S_{x y} & S_{z z} \end{matrix}] [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}]$

2.8 Vector Calculus using Cylindrical-Polar Coordinates

Calculating derivatives of scalar, vector and tensor functions of position in cylindrical-polar coordinates is complicated by the fact that the basis vectors are functions of position. The results can be expressed in a compact form by defining the gradient operator, which, in spherical-polar coordinates, has the representation

$\nabla \equiv (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z})$ $\nabla \equiv (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z})$

In addition, the nonzero derivatives of the basis vectors are

$\frac{\partial e_{r}}{\partial θ} = e_{θ} \frac{\partial e_{θ}}{\partial θ} = - e_{r} (all other derivatives are zero)$ $\frac{\partial e_{r}}{\partial θ} = e_{θ} \frac{\partial e_{θ}}{\partial θ} = - e_{r} (all other derivatives are zero)$

The various derivatives of scalars, vectors and tensors can be expressed using operator notation as follows.

Gradient of a scalar function: Let $f (r, θ, z)$ $f (r, θ, z)$ denote a scalar function of position. The gradient of f is denoted by

$\nabla f = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) f = e_{r} \frac{\partial f}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial f}{\partial θ} + e_{z} \frac{\partial f}{\partial z}$ $\nabla f = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) f = e_{r} \frac{\partial f}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial f}{\partial θ} + e_{z} \frac{\partial f}{\partial z}$

Alternatively, in matrix form

$\nabla f = {[\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial θ}, \frac{\partial f}{\partial z}]}^{T}$ $\nabla f = {[\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial θ}, \frac{\partial f}{\partial z}]}^{T}$

Gradient of a vector function Let $v = v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}$ $v = v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}$ be a vector function of position. The gradient of v is a tensor, which can be represented as a dyadic product of the vector with the gradient operator as

$v \otimes \nabla = (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}) \otimes (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z})$ $v \otimes \nabla = (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}) \otimes (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z})$

The dyadic product can be expanded $-$ $-$ but when evaluating the derivatives it is important to recall that the basis vectors are functions of the coordinate $θ$ $θ$ and consequently their derivatives may not vanish. For example

$\frac{1}{r} \frac{\partial}{\partial θ} (v_{r} e_{r}) \otimes e_{θ} = \frac{1}{r} \frac{\partial v_{r}}{\partial θ} e_{r} \otimes e_{θ} + \frac{v_{r}}{r} \frac{\partial e_{r}}{\partial θ} \otimes e_{θ} = \frac{1}{r} \frac{\partial v_{r}}{\partial θ} e_{r} \otimes e_{θ} + \frac{v_{r}}{r} e_{θ} \otimes e_{θ}$ $\frac{1}{r} \frac{\partial}{\partial θ} (v_{r} e_{r}) \otimes e_{θ} = \frac{1}{r} \frac{\partial v_{r}}{\partial θ} e_{r} \otimes e_{θ} + \frac{v_{r}}{r} \frac{\partial e_{r}}{\partial θ} \otimes e_{θ} = \frac{1}{r} \frac{\partial v_{r}}{\partial θ} e_{r} \otimes e_{θ} + \frac{v_{r}}{r} e_{θ} \otimes e_{θ}$

Verify for yourself that the matrix representing the components of the gradient of a vector is

$v \otimes \nabla \equiv [\begin{matrix} \frac{\partial v_{r}}{\partial r} & \frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r} & \frac{\partial v_{r}}{\partial z} \\ \frac{\partial v_{θ}}{\partial r} & \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r} & \frac{\partial v_{θ}}{\partial z} \\ \frac{\partial v_{z}}{\partial r} & \frac{1}{r} \frac{\partial v_{z}}{\partial θ} & \frac{\partial v_{z}}{\partial z} \end{matrix}]$ $v \otimes \nabla \equiv [\begin{matrix} \frac{\partial v_{r}}{\partial r} & \frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r} & \frac{\partial v_{r}}{\partial z} \\ \frac{\partial v_{θ}}{\partial r} & \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r} & \frac{\partial v_{θ}}{\partial z} \\ \frac{\partial v_{z}}{\partial r} & \frac{1}{r} \frac{\partial v_{z}}{\partial θ} & \frac{\partial v_{z}}{\partial z} \end{matrix}]$

Divergence of a vector function Let $v = v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}$ $v = v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z}$ be a vector function of position. The divergence of v is a scalar, which can be represented as a dot product of the vector with the gradient operator as

$\nabla \cdot v = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \cdot (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z})$ $\nabla \cdot v = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \cdot (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z})$

$\nabla \cdot v \equiv \frac{\partial v_{r}}{\partial r} + \frac{v_{r}}{r} + \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{\partial v_{z}}{\partial z}$ $\nabla \cdot v \equiv \frac{\partial v_{r}}{\partial r} + \frac{v_{r}}{r} + \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{\partial v_{z}}{\partial z}$

Curl of a vector function Let $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{z} e_{z}$ $v = v_{R} e_{R} + v_{θ} e_{θ} + v_{z} e_{z}$ be a vector function of position. The curl of v is a vector, which can be represented as a cross product of the vector with the gradient operator as

$\nabla \times v = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \times (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z})$ $\nabla \times v = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \times (v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z})$

The curl rarely appears in solid mechanics so the components will not be expanded in full

Divergence of a tensor function. Let $S$ $S$ be a tensor, with dyadic representation

The divergence of S is a vector, which can be represented as

$\nabla \cdot S = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \cdot (\begin{array}{l} S_{r r} e_{r} \otimes e_{r} + S_{r θ} e_{r} \otimes e_{θ} + S_{r z} e_{r} \otimes e_{z} \\ + S_{θ r} e_{θ} \otimes e_{r} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ z} e_{θ} \otimes e_{z} \\ + S_{z r} e_{z} \otimes e_{r} + S_{z θ} e_{z} \otimes e_{θ} + S_{z z} e_{z} \otimes e_{z} \end{array})$ $\nabla \cdot S = (e_{r} \frac{\partial}{\partial r} + e_{θ} \frac{1}{r} \frac{\partial}{\partial θ} + e_{z} \frac{\partial}{\partial z}) \cdot (\begin{array}{l} S_{r r} e_{r} \otimes e_{r} + S_{r θ} e_{r} \otimes e_{θ} + S_{r z} e_{r} \otimes e_{z} \\ + S_{θ r} e_{θ} \otimes e_{r} + S_{θ θ} e_{θ} \otimes e_{θ} + S_{θ z} e_{θ} \otimes e_{z} \\ + S_{z r} e_{z} \otimes e_{r} + S_{z θ} e_{z} \otimes e_{θ} + S_{z z} e_{z} \otimes e_{z} \end{array})$

$\nabla \cdot S \equiv [\begin{matrix} \frac{\partial S_{r r}}{\partial r} + \frac{S_{r r}}{r} + \frac{1}{r} \frac{\partial S_{θ r}}{\partial θ} + \frac{\partial S_{z R}}{\partial z} - \frac{S_{θ θ}}{r} \\ \frac{1}{r} \frac{\partial S_{θ θ}}{\partial θ} + \frac{\partial S_{r θ}}{\partial r} + \frac{S_{r θ}}{r} + \frac{S_{θ r}}{r} + \frac{\partial S_{z θ}}{\partial z} \\ \frac{\partial S_{z z}}{\partial z} + \frac{\partial S_{r z}}{\partial r} + \frac{S_{r z}}{r} + \frac{1}{r} \frac{\partial S_{θ z}}{\partial θ} \end{matrix}]$ $\nabla \cdot S \equiv [\begin{matrix} \frac{\partial S_{r r}}{\partial r} + \frac{S_{r r}}{r} + \frac{1}{r} \frac{\partial S_{θ r}}{\partial θ} + \frac{\partial S_{z R}}{\partial z} - \frac{S_{θ θ}}{r} \\ \frac{1}{r} \frac{\partial S_{θ θ}}{\partial θ} + \frac{\partial S_{r θ}}{\partial r} + \frac{S_{r θ}}{r} + \frac{S_{θ r}}{r} + \frac{\partial S_{z θ}}{\partial z} \\ \frac{\partial S_{z z}}{\partial z} + \frac{\partial S_{r z}}{\partial r} + \frac{S_{r z}}{r} + \frac{1}{r} \frac{\partial S_{θ z}}{\partial θ} \end{matrix}]$