Resolution of the Layer00 Silicon Detector for Various Configurations
A PS file of this information,
which is more suitable for printing is available.
Introduction
We have written a realistic simulation of a silicon detector
with p-strip readout,
in order to calculate the intrinsic resolution as a function
of crossing angle, intermediary strip, signal to noise, and strip pitch.
This information allows the silicon design to be optimised given
a certain modularity of the detector.
In section 2, the simulation is described.
In section 3, our results are given and discussed.
Our conclusions are presented in section 4.
Simulation of the silicon detector
The simulation of the silicon detector is performed with 5 variable
parameters:
The pitch of the readout;
The signal to noise ratio;
The presence or absence of an intermediary strip;
The angle of the track, $\alpha$;
The position of the track, $\eta$, on first entering the silicon.
By integrating over values of $\eta$ from 0 to the strip pitch, the resolution
can be determined as a function of crossing angle for a given pitch,
signal-to-noise and presence or absence of intermediary strip.
To simulate the response, the track is stepped through the silicon
in 1um steps, starting at the position $\eta$ and progressing at
an angle $\alpha$.
At each step, the total number of electron-hole pairs created is determined.
These are drifted to the collection side of the silicon, taking
account of diffusion and of the Lorenz angle. The charge is
divided between the readout strips and random noise added.
Each of these steps is now detailed followed by a description of the
algorithm used to reconstruct the particle position.
Landau Fluctuations
At each step, the total number of electron-hole pairs created is determined.
This is done by calculating the number of collisions
in $1\mu$m of silicon: a Poisson distribution of mean 4. Then for each
interaction, the energy losses are calculated according to~\cite{Bichsel}.
In 90\% of all collisions, the energy loss is less than 170eV, and the
mean energy loss for these collisions is 30eV. However in 2\% of cases,
it is greater than 1000eV, and in 0.2\% of cases, it is greater than 10000eV.
It is these high energy fluctuations which lead to the well known
quasi-Landau distribution for the sum of all energy losses in the silicon.
Since these large fluctuations occur rarely, they cause biases in the
position determination on an event-by-event basis. Over many events, this
leads to a broadening in the resolution.
Diffusion
The holes are allowed diffuse to the surface according to the model
of Belau et al.~\cite{belau}, which takes account of both the broadening
of the cloud of holes and of the Lorenz angle, which for a field of
1.4 Tesla, causes the holes to drift at an angle of $2.7^o$.
We have assumed a full depletion voltage
of 50V for the silicon, and an operating voltage of 60V.
We have verified that our simulation gives the same results as
presented in this paper for the same operating conditions.
This model has in turn been checked against data.
Charge Division
Having diffused the holes to the surface of the silicon, the charge is
divided according to which strip it is nearest to.
In the case that we have an intermediary strip, 80\% of the charge on this
strip is split between its two neighbours.
Noise
In order to simulate a signal-to-noise ratio of $S:N$,
noise is added randomly to each strip assuming it comes from a Gaussian
distribution with a sigma of $N$, where the most probable value of the Landau
has a value $S$.
Reconstruction
The algorithm used to reconstruct the position of the particle
proceeds by scanning for the strip with the highest signal,
provided that signal is greater than 3:1. Its highest neighbour
is taken, provided its signal is greater than 1.5:1. Then the position
is determined by $\eta=R/(L+R)$ where $L,R$ are the left and right most
strips.
This algorithm works well for small angles but is quite poor at large
angles. Consequently, for crossing angles greater than $15^o$, we
have used an algorithm as described by the DELPHI collaboration~\cite{delphi}.
All strips greater than 2:1 about the highest signal are taken
and the position is the midpoint between the first and last channels
of the cluster, corrected with
$$
\omega=\bigl[min(S_{first},\bar S)-min(S_{last},\bar S)\bigr]/(2\bar S)
$$
where $\bar S$ is the average pulse-height of all channels in between.
|
The effect that each of the ingredients in our simulation has on
the calculated resolution is shown in this figure.
Turning on diffusion improves the resolution at small angles.
The Lorenz angle shifts the distribution, while the Landau distribution
degrades the resolution, particularly at large angles.
|
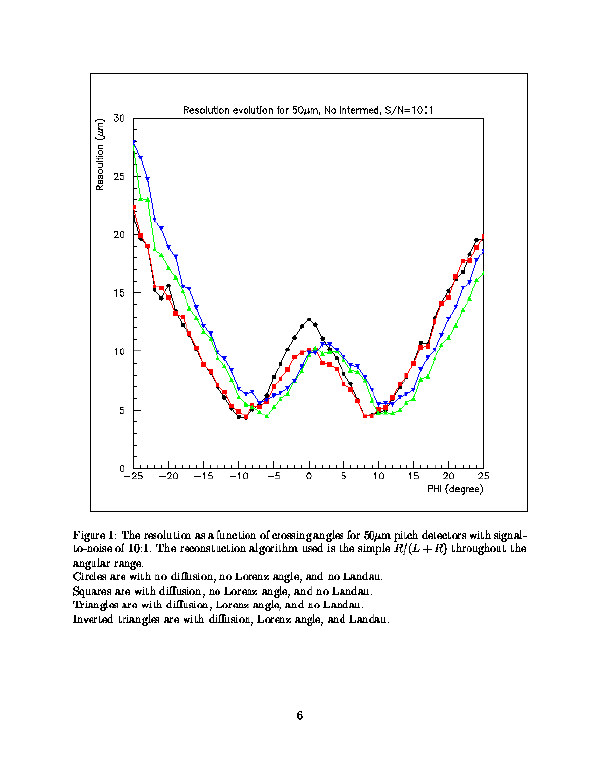
|
Results
We have calculated the resolution as a function of crossing angle
for:
strip pitches of 50,60,70,80,90,100$\mu$m;
with and without intermediary strips;
for signal-to-noise ratios of 10:1 and 13:1, which were
chosen as worst case and average case scenarios, based on the
likely cable lengths and chip parameterisation at our disposal as of
25.11.98.
|
This figure shows the resolution for a $50\mu$m pitch detector
with S:N of 13:1, with and without an intermediary strip.
|
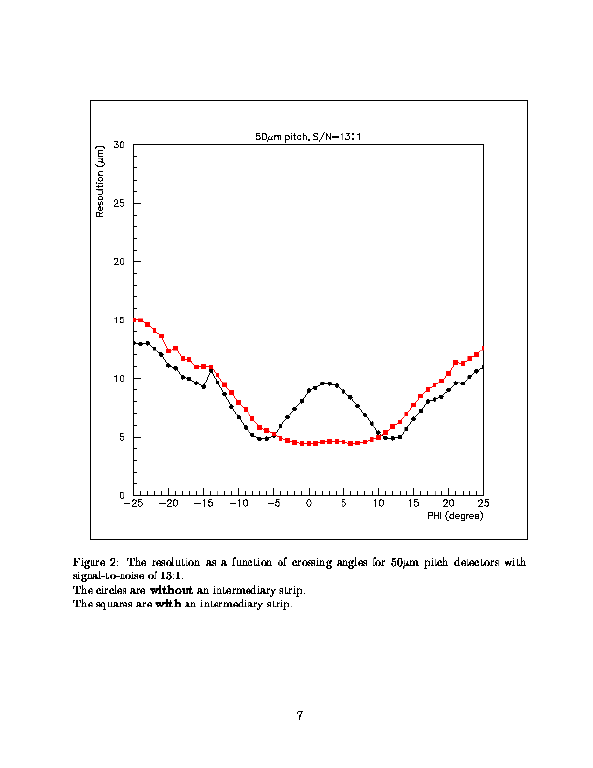
|
Four points are noteworthy:
firstly, for angles $<\approx 7^o$,
the intermediary strip plays an important role;
secondly, for angles
$>\approx 7^o$, the intermediary strip would degrade the resolution by
1 to $2\mu$m;
thirdly, the effect of the Lorenz angle is evident.
fourthly, for angles greater than about $12^o$, the resolution degrades
rapidly.
|
The figure shows the same plot but repeats it
for $50,60,70,80\mu$m
detectors as indicated. The behaviour in each case is similar.
The angular range, over which an intermediary strip is useful,
broadens as the pitch increases. In all cases, the resolution
degrades rapidly for angles greater than $15^o$.
|
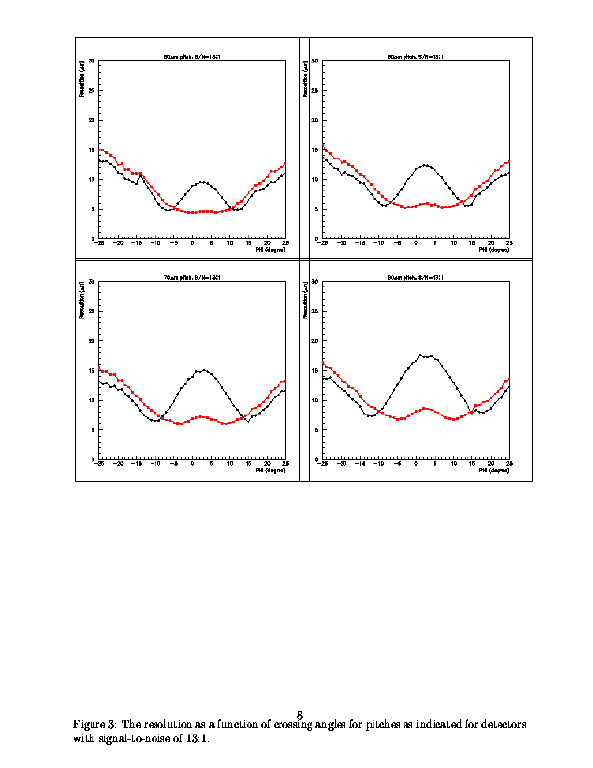
|
|
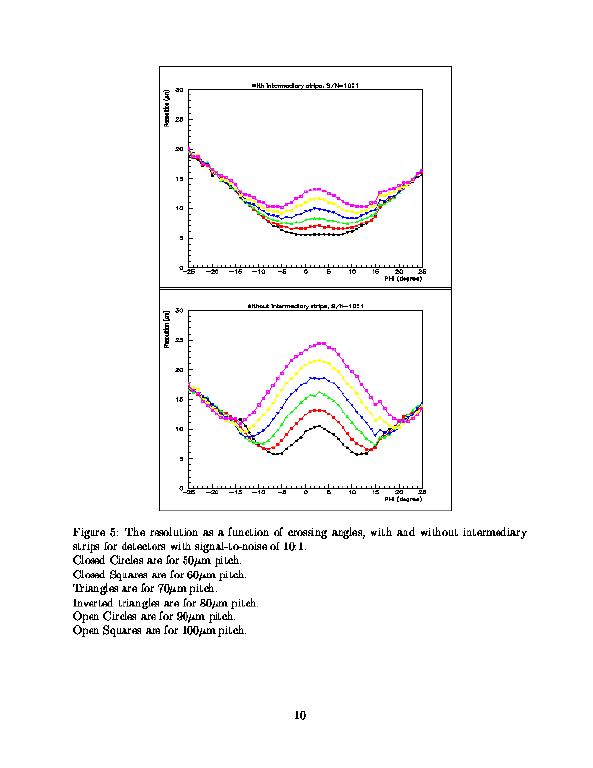
Here are the same plots for $50,60,70,80,90,100\mu$m
pitch, with and without intermediary strips, but this time for a
signal-to-noise of 10:1. It is noted that for small angles
the degradation (with respect to S/N of 13:1)
is small, about $1\mu$m, but for larger angles it is much bigger, up to
$5\mu$m. This is a consequence of the fact that in spreading itself
over more strips, the charge per strip begins to be obscured by the noise.
If we are led to mechanical designs which require longer cable lengths,
as now seems likely, then the noise will be worse than had been envisaged,
and the resolutions at large angles will be particularly affected.
|
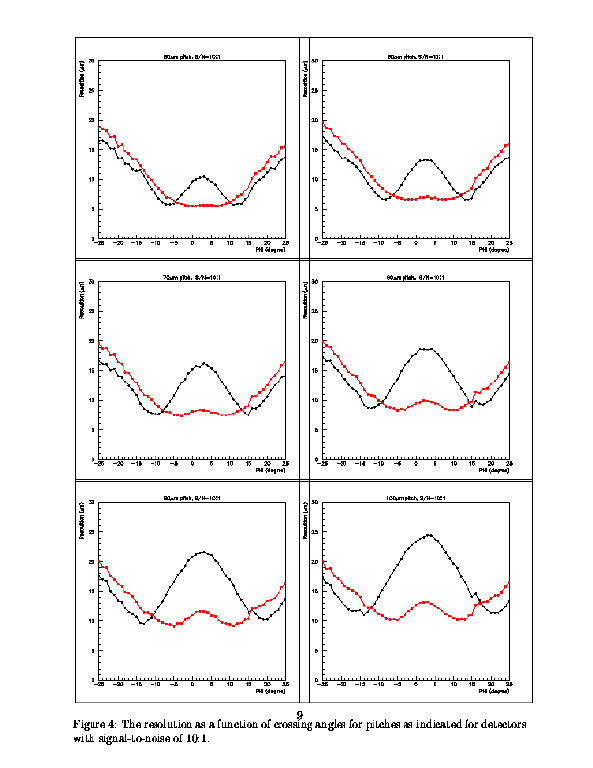
|
|
This is a summary of the plots for each pitch {\it with}
and {\it without} an intermediary strip.
We note an important point:
Above about $15^o$, the resolution is {\bf insensitive} to the strip
pitch, and furthermore, it is better {\bf not} to use an intermediary
strip here.
|
|
Resolutions for three geometries
With these plots, we can now calculate the response of any mechanical
design in terms of the resolution we would expect.
We have done this for three cases:
Firstly, for an 8-fold detector with $50\mu$m read-out pitch with
an intermediary strip. This was the favoured design as of 25.11.98.
Secondly, for a 12-fold detector with $70\mu$m read-out pitch with
an intermediary strip. This would be the naive basic design if we
were to go to a 12-fold modularity, whether to gain resolution,
reduce readout, or for triggering purposes.
Thirdly, for a 12-fold detector with varying pitches. We have used
our results to perform an optimisation for the best average resolution,
subject to the constraint that 128 channels span 9432$\mu$m, the width
of detector required for a 12-fold geometry with 10\% overlaps.
Our solution requires starting off with
$90\mu$m pitch-no-intermediary for the
first 3 strips, changing to $80\mu$m pitch-no-intermediary for the next 15,
changing to $80\mu$m pitch-with-intermediary for the next 25,
changing to $70\mu$m pitch-with-intermediary for the next 6,
changing to $60\mu$m pitch-with-intermediary for the next 5,
and finally $50\mu$m pitch-with-intermediary until the centre of the detector. The pattern
is repeated on the other side.
|
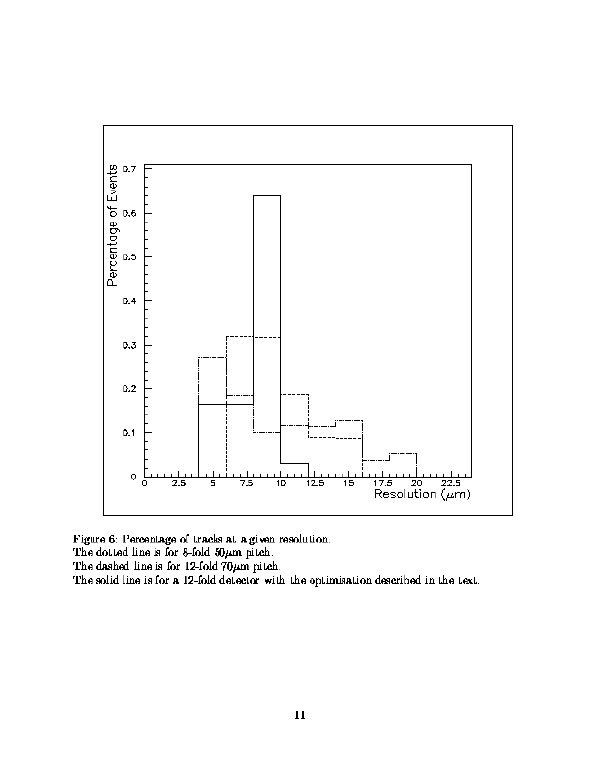
This plot shows the result of these configurations.
8-fold modularity with $50\mu$m pitch is clearly the worst.
Although having the greatest number of tracks with $5\mu$m resolution
it has long tails.
15\% of all tracks have resolutions greater than $15\mu$m and
45\% have resolutions greater than $10\mu$m.
This is due principally to the poor resolution at large crossing
angles.
12-fold modularity with $70\mu$m pitch is better.
5\% of tracks have resolutions worse than $15\mu$m and
38\% of tracks have resolutions worse than $10\mu$m.
However, the best solution is obtained with our optimisation technique.
Now less than 5\% of tracks have resolutions worse than $10\mu$m
and in addition the response is more uniform over the detector.
|
|
Efficiencies
A further consideration is the efficiency for reconstucting
clusters, especially important if Layer00 might be used in the trigger.
For the 8-fold geometry, the efficiency is 99.5\% assuming a
signal-to-noise of 10:1.
We have also examined the efficiency for a worst-case-scenario of
7:1 corresponding to 3000 e.n.c.
For the 8-fold geometry with $50\mu$m pitch and an intermediary strip,
the efficiency would deteriorate to 87\%, while
for our optimised 12-fold geometry described above, it would remain
higher than 99\%.
If it was necessary to run with a single strip threshold of 4 to 1,
(rather than 3 to 1,) in order to suppress noise, then the efficiency
for the 8-fold geometry deteriorates to 60\%, while for the
optimised 12-fold geometry, it would be 94\%.
Conclusions
We have produced a simulation which allows us to calculate the
resolution of detectors of different modularity and strip pitches.
In addition, it lets us optimise the strip pitches for a given
mechanical design.
A number of important points have been established.
It is extremely beneficial to use an intermediary readout strip
at small angles ($<7^o$).
It is better {\it not} to use an intermediary strip at larger
angles, especially if we have poor signal-to-noise
For large angles ($>15^o$), the resolution is independent of
readout pitch.
For large angles ($>15^o$), the resolution is poor ($>10\mu$m).
For this reason, unless there are overwhelming mechanical reasons,
we would advise against an 8-fold geometry. This is especially
true if the detector is to be used in the trigger.
At the present time, the best design would appear to be of 12-fold modularity
with a variable readout pitch from $50\mu$m in the centre to $90\mu$m
at the edges. This also ties in well with the number of readout chips,
the cable lengths, and the triggering modularity of SVX.
Bibliography
H.\ Bichsel, ``Inelastic electronic collision cross sections for
Monte Carlo calculations.'' {\it Nucl.\ Inst.\ and Meth.\ }{\bf B}52 (1990) 136.
Belau et al., ``Charge Collection in Silicon Strip Detectors''
{\it Nucl.\ Inst.\ and Meth.\ }214 (1983) 253.
V.\ Chabaud, ``The DELPHI Silicon Strip Microvertex
Detector with Double Sided Readout'' CERN-PPE/95-86.





